Trigonometry is a branch of mathematics that deals with the relationship between the ratio of the sides with the corresponding angle in a triangle. The triangle we are talking about here is right-angled.
There are three main functions in trigonometry; they are Sine (Sin), Cosine(Cos) and tangent(tan). And using these main functions, the other functions like Cosecant, secant and cotangent are derived. Most of the trigonometric concepts are based on these functions. These trigonometric functions are used to calculate unknown angles and distances from known or measured angles.
For example, if you know the length of two sides of a triangle(right-angled triangle) and the enclosed angle, then the length of the third side and measure of the two remaining angles can be easily calculated.
Trigonometric Ratios Of A Right Angled Triangle
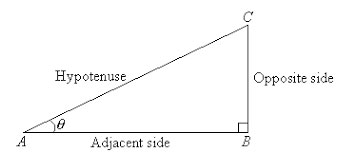
Figure 1: A right-angled triangle
A right-angled triangle shown in Figure 1, has the following three sides.
The opposite Side, also called Perpendicular, is the side opposite to the angle θ i.e. BC
The adjacent Side also called the base, is the adjacent side to the angle θ, i.e. AB
The hypotenuse is the side that is opposite to the right angle, i.e. AC
In right-angled triangle △ ABC
Adjacent Side = AB
Opposite Side= BC
Hypotenuse = ACLet us define the following ratios, which are also called Trigonometric Ratios for .
Trigonometric Ratio Table:
The Trigonometry Ratio Table is as follows:
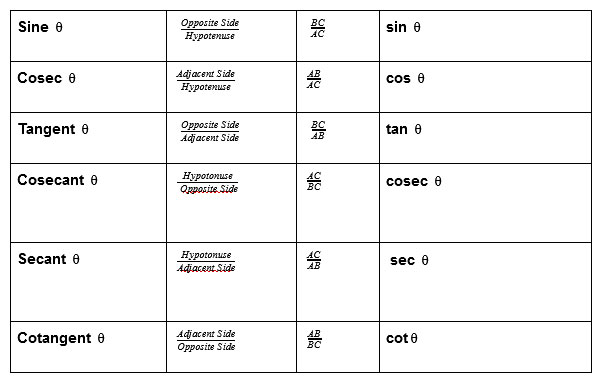
The ratios mentioned above are abbreviated as sin, cos, tan, cosec, sec, and cot, respectively. It is worth noting that the ratios cosec, sec, and cot are the reciprocals of the ratios sin, cos, and tan, respectively.
So, the trigonometric ratios of an acute angle in a right-angled triangle define a relationship between the angle and the length of its sides.
(i) cot θ = 1tan (ii) sec θ = 1cos (iii) cosec θ = 1sin
Solved Examples on Trigonometric Ratios:
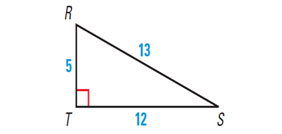
Example 1: Find the sin, the cos, and the tan functions of the indicated angle.
(i). ∠S
(ii) ∠R
First, let us solve for S
hypotenuse =13
length of the opposite side = 5,
length of the adjacent side =12.
Sin S = opposite side. / hypotenuse. = 5 / 13 ≈ 0.3846
Cos S = adjacent side / hypotenuse. = 12 / 13 ≈ 0.923
Tan S = opposite side / adjacent side = 5 / 12 ≈ 0.4167
Solving for (ii) ∠R
hypotenuse =13
length of the opposite side =12,
length of the adjacent side = 5.
Sin R = opposite side. / hypotenuse. = 12 / 13 ≈ 0.9231
Cos R = adjacent side / hypotenuse = 5 / 13 ≈ 0.3846
Tan R = opposite side / adjacent side = 12 / 5 ≈ 2.4
Solved Example 2
In the case where tan A = 3/4, find the other trigonometric ratio of A.
Solution
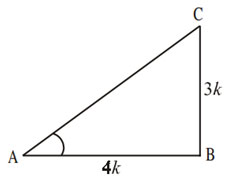
Given tan A = 3/4
Hence tan A = Opposite side/Adjacent side = 3/4
For angle A , opposite side(BC)= 3k
Adjacent side = 4k ( k is always positive)
Now, we have in triangle ABC (by Pythagoras theorem)
Use the Pythagoras Theorem and find the hypotenuse
AC2=AB2 + BC2
= (4k)2 + (3k)2
= 16k2 + 9k2
AC2 =25k2
Taking square root on both side
AC= 5k
So hypotenuse = 5k
So now we can write the other ratios of trigonometry
Sin A = opposite side / hypotenuse = 3k / 5k = 3 / 5
Cos A = adjacent side / hypotenuse = 4k / 5k = 4 / 5
Tan A = opposite side / adjacent side = Sin A / Cos A = 3k / 4k = 3 / 4
And also
Cosec A = 1 / sin A = 5 / 3
Sec A = 1 / cos A = 5 / 4
Cot A = 1 / tan A = 4 / 3
Trigonometric Function Table
Trigonometric tables can be used to determine the trigonometric ratios for standard angles such as 0°, 30°, 45°, 60°, and 90°. The trigonometric table contains trigonometric ratios: sine, cosine, tangent, cosecant, secant, and cotangent. Sin, cos, tan, sec, cosec, and cot are abbreviations for these ratios. Trigonometric ratios of standard angles are critical to solving trigonometry issues.
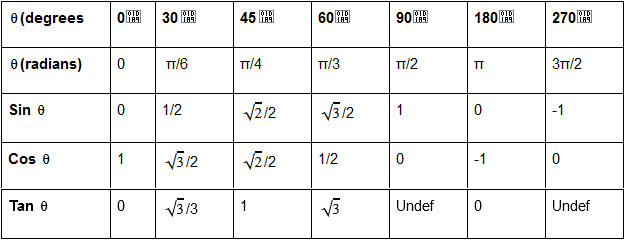
Undef: Not defined
Trigonometric Ratio for Complementary Angles
Complementary angles are pairs of angles when added equals 90° They are 40° and 50°, 60° and 30°, 20° and 70°, 15° and 75°, and so on.
So now the formula will be as follows
cos θ = sin (90° – θ)
tan θ = cot (90° – θ)
sin θ = cos (90° – θ)
cosec θ = sec (90° – θ)
cot θ = tan (90° – θ)
sec θ = cosec (90° – θ)
The trigonometric table contains a few crucial points that should be noticed.
- The values for complementary angles in a trigonometric table, such as 30° and 60°, may be obtained using complementary formulae for the different trigonometric ratios.
- According to a trig table, various ratios are either specified as “Undefined.” This is because when the values are computed, the numerator appears as a zero, rendering them undefined.
- Various trig ratio values in a trigonometry table have sign shifts under 180°, 270°, etc. The reason is that the quadrant has shifted.
Trigonometry Formulas
Involving Sum and Difference Identities
The sum and difference identities include the trigonometry formulas of sin(x + y), cos(x – y), cot(x + y), etc.
- sin(x + y) = sin(x)cos(y) + cos(x)sin(y)
- cos(x + y) = cos(x)cos(y) – sin(x)sin(y)
- tan(x + y) = (tan x + tan y)/(1 – tan x • tan y)
- sin(x – y) = sin(x)cos(y) – cos(x)sin(y)
- cos(x – y) = cos(x)cos(y) + sin(x)sin(y)
- tan(x − y) = (tan x – tan y)/(1 + tan x • tan y)
Trigonometric formulas based on the relationship between different trigonometric ratios that will help you memorize the trigonometric table.
- sin x = cos (90° – x)
- cos x = sin (90° – x)
- tan x = cot (90° – x)
- cot x = tan (90° – x)
- sec x = cosec (90° – x)
- cosec x = sec (90° – x)
- 1/sin x = cosec x
- 1/cos x = sec x
- 1/tan x = cot x
Pythagorean Identities
- sin²θ + cos²θ = 1
- tan2θ + 1 = sec2θ
- cot2θ + 1 = cosec2θ
- sin 2θ = 2 sin θ cos θ
- cos 2θ = cos²θ – sin²θ
- tan 2θ = 2 tan θ / (1 – tan²θ)
- cot 2θ = (cot²θ – 1) / 2 cot θ
Though the Trigonometric ratios and formulas look a little tricky, you will be able to master any problems involving trigonometry with a lot of practice.
Conclusion
Trigonometry is extremely beneficial in identifying an unknown side of a triangle. The notion of the right triangle in trigonometry is extremely successful and applied in various fields to compute angles and distance in map-making, surveying, artillery range finding, satellite navigation, medical imaging, oceanography, seismology, architecture, astronomy and geography, to name a few.

Namaste UI collaborates closely with clients to develop tailored guest posting strategies that align with their unique goals and target audiences. Their commitment to delivering high-quality, niche-specific content ensures that each guest post not only meets but exceeds the expectations of both clients and the hosting platforms. Connect with us on social media for the latest updates on guest posting trends, outreach strategies, and digital marketing tips. For any types of guest posting services, contact us on info[at]namasteui.com.

